Visual Representations In Primary Maths
By: Judy Zorfass, Angela Han, and PowerUp WHAT WORKS
Images/representations of numbers 1-10 for use in display and as images to support work and conceptual understanding.
Introduction
All students can benefit from using visual representations, although struggling students may require additional, focused support and practice. Visual representations are a powerful way for students to access abstract mathematical ideas. To be college and career ready, students need to be able to draw a situation, graph lists of data, or place numbers on a number line. Developing this strategy early during the elementary grades gives students tools for engaging with—and ways of thinking about—increasingly abstract concepts. Over time, they will work toward developing Common Core Standards for Mathematical Practice:
- CCSS.Math.Practice.MP2 Reason abstractly and quantitatively.
- CCSS.Math.Practice.MP4 Model with mathematics.
- CCSS.Math.Practice.MP5 Use appropriate tools strategically.
- In teaching addition and subtraction, there has been a clear use of visual representations such as number squares and number lines, with number lines being viewed as the most appropriate representation for demonstrating the characteristics of these operations, for visualising the calculations and for developing flexible ways of executing the operations.
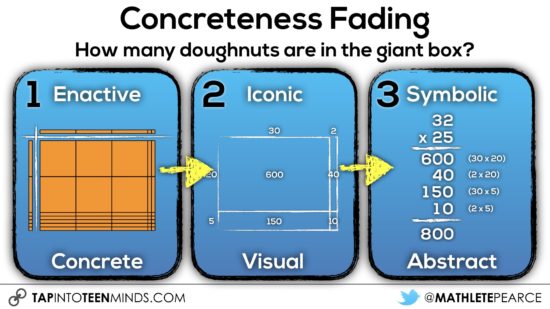
- Visual representation is often used in a three-step instructional approach called concrete-representational-abstract, or CRA. (Some teachers call this approach concrete-pictorial-abstract.) When you teach math concepts this way, you start by using concrete manipulatives, like showing an addition problem with Unifix cubes.
WAYS TO SUPPORT STUDENTS
Helping students choose the 'right' visual representation often depends on content and context. In some contexts, there are multiple ways to represent the same idea. Show your students a variety of examples in order to demonstrate when (and why) they should choose each one (see UDL Checkpoint 2.5: Illustrate through multiple media). Consider how you could use the following strategies to support your students:
- Check for understanding to determine a starting point. For example, you could ask the following questions: Why do you think that? How do you know that is correct? How does that picture represent the problem? Can you explain your answer? Is there another way you could do that?
- Ask students about features of the visual representation (including labels and scales, when appropriate).
- As students create visual representations, ask questions to ensure that they understand all the features of the representations. Prompt students to focus on the information the visual representations provide.
- When possible, include alternative visual representations and discuss the similarities and differences between them.
- Vary the shapes and orientations of representations so that students focus only on the important features as they learn about the objects and situations represented.
- Show your students a specific representation—a graph or a table—that is missing an important feature. Ask them to identify the missing feature.
Drawing on technology tools
New technologies are constantly expanding our ability to visualize data and explain mathematical concepts. For teachers looking to incorporate technology into the classroom, using virtual manipulatives (instead of physical ones) can be a good start. Students can begin with simple graphical representations of mathematical concepts and then work toward more complex modules that require them to create the data or work within a system of rules, like a game. Infographics—visualizations that are designed to communicate complex information effectively—have become increasingly popular. They can be used to 'tell a story' with numbers, such as international democracy rankings or climate change impacts. Learning to create infographics gives students additional tools to communicate data and other quantitative information.
3D printing is a technology that, until recently, has been too expensive to make use of in a classroom. However, thanks to falling prices, they have now started to appear in high schools and it may not be long before elementary schools and middle schools also embrace this technology. 3D printing allows you to create solid, three-dimensional models from a digital design. You can explore what others have created to get a sense of what is possible. Imagine having students design and create their own mathematical models and manipulatives!
For more ideas on using technology to create visual representations, visit the Tech Matters blog or PowerUp's Pinterest page. You can also check out the 'Virtual Manipulatives' video, which supports students' use of visual representations.
In the classroom
Geometry lends itself naturally to teaching with visual representations, as can be seen in Ms. Richardson's Grade 6 class. So far, students have learned how to classify different quadrilaterals and triangles, and they are beginning to decompose polygons. They have also started using software (e.g., GeoGebra) that can support their understanding by emphasizing the connections between mathematical language and visualization.
Ms. Richardson's lesson objective is to have students decompose polygons into triangles, rectangles, and trapezoids. She will address two s Common Core State in this lesson:
- CCSS Math 6.G.1 Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing into rectangles or decomposing into triangles and other shapes; apply these techniques in the context of solving real-world and mathematical problems.
- CCSS Math MP4 Model with mathematics.
Ms. Richardson has students work on these standards within the context of a real-world example—a painting by the artist Sol LeWitt.
Sol LeWitt. Wall Drawing #1113. On a wall, a triangle within a rectangle, each with broken bands of color, 2003. Hirshhorn Museum and Sculpture Garden, Smithsonian Institution.
Students will build on their existing technology skills and create a model of this work, decomposing polygons and creating their own virtual LeWitt in the process. Ms. Richardson's lesson plan is organized into three sections: a warm-up exercise to review concepts, the main learning task, and a closing discussion and assessment.
Lesson plan
| Launch |
|
|---|---|
| Learning Task |
|
| Closure |
|
Online resources for visual representations

This article draws from the PowerUp WHAT WORKS website, particularly the Visual Representations Instructional Strategy Guide. PowerUp is a free, teacher-friendly website that requires no log-in or registration. The Instructional Strategy Guide on visual representations includes a brief overview with an accompanying slide show; a list of the relevant mathematics Common Core State Standards; evidence-based teaching strategies to differentiate instruction using technology; short videos; and links to resources that will help you use technology to support mathematics instruction. If you want to dig deeper into the research foundation behind best practices in the use of virtual manipulatives, take a look at our Tech Research Brief on the topic. If you are responsible for professional development, the PD Support Materials provide helpful ideas and materials for using the resources. Want more information? See PowerUp WHAT WORKS.
Judy Zorfass, Angela Han, and PowerUp WHAT WORKS (2014)
Visual representations (VRs) are used in mathematics to help students solve problems or understand abstract ideas. Graphing data, placing numbers in a line, or drawing out a word problem are all examples of using VRs. Several NSF-funded projects within the DRK–12 portfolio are using VRs to enhance mathematical understanding. In this Spotlight, CADRE asks five mathematics education projects to explain how they use VRs in their research and development.
CAREER: Algebraic Knowledge for Teaching: A Cross-cultural Perspective (Grades: 1-4)
1. How and why is the role of VRs critical in the model or intervention being designed and/or tested by your project?
VR plays a critical role in the Algebraic Knowledge for Teaching: A Cross-cultural Perspective project. The goal of the project is to glean useful algebraic knowledge for teaching (AKT) based on US and Chinese expert elementary teachers’ mathematics classroom instruction. We focused on three aspects of AKT, including teachers’ use of representations. In particular, we are interested in the role of concrete representations—including VRs—and their connection to abstract representations. As such, VRs play a critical role in identifying effective AKT in this project, and serve as a key aspect of the project intervention.
2. Do you have example representations? How were these representations implemented within your project?
One critical type of VR emphasized by our project is linear quantity models, such as the “tape diagram.” This type of representation has been widely used in East Asian countries due to its effectiveness in representing quantitative relationships to enhance students’ problem solving. As such, this model is also emphasized by the Common Core State Standards. In our project, we identified teaching segments that involved the use of tape diagrams and other related linear quantity models such as “pre-tapes” (linear arrangements of discrete objects) and number lines. We then compared how these linear quantity models are used in US and Chinese classrooms.
3. What aspects of the use of VRs were being tested or how were they connected to the research questions being explored?
Given that one of our project research questions relates to teachers’ use of representations, our analysis of linear quantity models is highly relevant. Focusing on linear quantity models, we analyzed the types, contexts, and purpose of teachers’ use of VRs in US and Chinese classrooms. We also examined the ways that students engage in this process of modeling. Findings about cross-cultural differences in using linear quantity models have been shared with the project participants through summer workshops (the project’s intervention section). Teachers then retaught their lessons based on the advice given during the intervention.
4. Do you have any emerging findings to share?
Our research has revealed rich opportunities for additional use of linear quantity models in US classrooms. However, the major difference in the existing use of these models between the sampled US and Chinese lessons lies in the instructional purpose for which these models are employed. Whereas Chinese lessons used linear quantity models (including pre-tapes) for the sole purpose of modeling the underlying quantitative relationships of story problems, US lessons used linear representations (in both contextual and noncontextual problems) mainly for the purpose of directly obtaining answers (e.g., counting the pre-tapes to obtain the answer, distributing dots to a given tape to obtain the answer, jumping on a number line to obtain the answer). On those occasions when the linear quantity models are used to represent the problem situations in US classrooms, these models are often only used to target the individual quantities rather than the interactions between them (i.e., the quantitative relationships). In addition, US teachers in this study rarely involved students in discussions of linear models; yet, Chinese teachers spent significant time engaging students in co-constructing, gesturing, comparing, and explaining these models. Together, these findings call for rethinking the purpose for which VRs are used, and finding new ways to engage students with VRs in US classrooms.
Project Resources & Products:
- The comparative work on teachers’ use of linear quantity models is currently under revision for resubmission to a research journal.
- A study on Chinese teachers’ use of tape diagrams will be published in Teaching Children Mathematics.
- The project has created 25 annotated US and Chinese video clips illustrating cross-cultural differences in using VRs.
- Our video in the 2016 NSF Video Showcase briefly mentioned cross-cultural differences in VRs.
Developing Formative Assessment Tools and Routines for Additive Reasoning (Grades: K-3)
1. How and why is the role of VRs critical in the model or intervention being designed and/or tested by your project?
VRs play a central role in the learning progressions for number, addition, and subtraction in grades K–3 that we have developed and field tested through our DRK–12 project Developing Formative Assessment Tools and Routines for Additive Reasoning. Structured bead strings, ten frames, number paths, number lines, and open number lines are used in our project to support students in developing conceptual understanding of number, addition, and subtraction. More importantly, they provide an instructional bridge to move students from concrete counting strategies to more abstract addition and subtraction strategies based on a strong foundation of number sense.
Research from the Freudenthal Institute has shown that the empty or open number line can help students develop more-sophisticated strategies for addition and subtraction through a process of progressive mathematization. However, to use a number line, children must understand its attributes (e.g., quantity is represented as length or distance; it is a continuous model; between any two numbers there are more numbers that are not shown). Building on the work of Adri Treffers, we build understanding of the empty or open number line from children’s understanding of counting by using a structured bead string (e.g., 100 beads with groups of 10 beads in alternating colors). Teachers learn how to use the bead string to have children locate numbers, develop more sophisticated counting strategies (e.g., counting or adding by tens), and then transfer that understanding to a number path and open number line. Here is an example of how to transfer understanding of difference on the bead string to subtraction on the open number line.
We provide teachers with explicit training in the use of these visual models and in their role in the development of student understanding. Teachers learn how to incorporate concrete and visual models into their instruction, recognize the models and their purpose in their curriculum materials, and use formative assessment items that ask children to interact with visual models to continually assess and respond to students’ developing understanding.
2. Do you have example representations? How were these representations implemented within your project?
The OGAP Framework for Additive Reasoning includes learning progressions for number, addition, and subtraction. This framework is central to the OGAP formative assessment system—teachers develop understanding of the learning progressions through professional development and then use the framework to select formative assessment items, analyze student work, and respond instructionally to the evidence they see in student work. You can see the importance of visual models in the transitional levels.
TheOGAPNumber Line Continuum is a tool teachers use to understand how they can build students’ understanding and fluency with number lines, moving from a concrete understanding of counting by ones, to unitizing in groups, to developing base-10 understanding and strategies for addition and subtraction.
We have developed over 300 formative assessment items (some of which incorporate visual models) that teachers use to assess their students’ understanding of visual models. The online item bank, and many other resources, are available for teachers to use once they have gone through our training.
3.What aspects of the use of VRs were being tested or how were they connected to the research questions being explored?
Our progressions are continually revised to reflect the evidence we see in student work from our piloted formative assessment items. (The number progression is currently under revision based on evidence of students’ use of visual models to make sense of counting, comparison, and relative magnitude tasks.) Research on teachers’ use of these tools and routines to make sense of and respond instructionally to student thinking is ongoing. The findings from this research are being used to both improve the tools and routines and also to learn more about the affordances and constraints of the tools and routines for formative assessment in school settings.


4. Do you have any emerging findings to share?
We are still in the development cycle and in the process of collecting and analyzing data for ongoing research. Here are some emerging findings in relation to VRs:
- Visual models play a key role in bridging students’ understanding of (1) number as a collection of ones to more sophisticated understanding of number as being composed of place value parts, and (2) counting to additive reasoning and to the development of more sophisticated addition and subtraction strategies.
- Children’s underlying understanding of number, addition, and subtraction is evidenced by the strategies they use when interacting with VRs.
- These findings are reflected in our progressions and provide guidance for teachers to respond instructionally to evidence of student thinking and support the development of additive reasoning.
- Teachers have not had many opportunities to learn about research on how young children learn mathematics or delve deeply into the content at grades K–2. Professional development on these topics and on the use of visual models helps to inform their instruction and the use of their curriculum materials.
Project Resources & Products:
- A suite of tools and resources is available to trained teachers on the project website: http://www.ogapmath.com/resources-for-ogap-schools
- We submitted a manuscript on base-10 understanding to the NCTM journal Teaching Children Mathematics.
- We presented at the Psychology of Mathematics Education North American Chapter 2017 Annual Conference and will be presenting at both the NCSM and NCTM national conferences April 23–25.
INK-12: Teaching and Learning Using Interactive Ink Inscriptions in K-12 (Grades: 3-5)
1. How and why is the role of VRs critical in the model or intervention being designed and/or tested by your project?
VRs of mathematical concepts are the core of the INK–12 projects. We implemented a software system, Classroom Learning Partner (CLP), in which elementary students could create VRs of multiplicative situations using a combination of digital tools and freehand drawing.
2. Do you have example representations? How were these representations implemented within your project?
There were three main representational tools: stamps (multiple copies of identical images), number lines, and arrays, each of which provided mathematical structure as well as many options to the student user. Examples of all of our representations are on our website, INK-12.mit.edu. They are free to use and be shared.
3.What aspects of the use of VRs were being tested or how were they connected to the research questions being explored?
Our project was doing design-based research to a large extent, trying to see which kinds of representations would best support student thinking about multiplication and division. We were also exploring how to design representations that both gave students a certain amount of expressive freedom and had enough structure that we could analyze the student work automatically to find usage patterns.
4. Do you have any emerging findings to share?
Our publications lay out a variety of findings. The most overarching (which we’re still writing up) is that in a five-week trial in a fourth-grade classroom with two control classrooms, students who used our software had significantly higher gain scores than the control students.
Project Resources & Products:
- Publications and the software are downloadable from our website: INK-12.mit.edu
- We have developed a PDF of documentation for using the tools.
Mathematical Learning via Architectural Design and Modeling Using E-Rebuild (Grades: 6-8)
1. How and why is the role of VRs critical in the model or intervention being designed and/or tested by your project?
In the project Mathematical Learning via Architectural Design and Modeling Using E-Rebuild, we examined a game-based learning platform that enables multiple encoding or multimodal representation of mathematical problem solving for middle school students. 3-D dynamic visual–spatial representation is a core facet of the transformation and coordination of multimodal external representations in E-Rebuild. This project is aimed to engage students in meaningful interactions with a system of multimodal (e.g., verbal, notational, and visual–spatial), external representations, which in turn foster in students the performance of multiple encoding and the construction of a coordinated system of international representations of mathematical problems.
2. Do you have example representations? How were these representations implemented within your project?
Students actively process (e.g., interpret the 2-D and 3-D visual depictions of the architectural items and feedback) and maneuver the dynamic visualizations (e.g., build and construct visualized 3-D game objects) through a game-based learning platform while using mathematics and problem solving. Demo games are available at https://mileresearch.coe.fsu.edu/erebuildweb/
3. What aspects of the use of VRs were being tested or how were they connected to the research questions being explored?
Users’ gameplay behaviors (including VR-interaction behaviors) were recorded and a systematic behavior analysis was conducted to explore their interaction with the VRs and the associated learning processes.
4. Do you have any emerging findings to share?
We are still conducting data analyses, with two journal manuscripts submitted and under review.
Project Resources & Products:
- Demo games are available at https://mileresearch.coe.fsu.edu/erebuildweb/
Proportions Playground: A Dynamic World to Support Teachers' Proportional Reasoning (Grades: 6-7)
1. How and why is the role of VRs critical in the model or intervention being designed and/or tested by your project?
This intervention is about how teachers understand and learn from dynamic VRs. The Proportions Playground project arose from our observation that teachers reasoned differently about proportional situations when they were presented in a dynamic environment from when they were presented using paper and pencil. We decided that this was something worth understanding better, so we built a set of interactive “toys” (Web-based) designed to help teachers explore particular aspects of proportional reasoning.
What Is A Visual Representation
2. How were these representations implemented within your project?
The representations will be used in a three-day professional development setting in which we are focusing on some of the big mathematical ideas related to proportional reasoning. We will have teachers play with each of the representations and then solve at least one task with each. As part of this effort, we will also be asking participants to generate one or two additional (static) representations that describe the relationship of interest from the dynamic settings. The goal is to engage teachers in such a way that they can develop their understanding of proportions, draw connections between and among representations, and promote communication, conjecture making, and argument about mathematical ideas.
Visual Representations In Primary Maths Gcse
3. What aspects of the use of VRs were being tested or how were they connected to the research questions being explored?
Our focus is on how teachers interact with the dynamic VRs. Specifically, we are asking how teachers reason with the representations and how they use their proportional understandings to make sense of the situations. We are also interested in finding evidence that participants are making connections between different fine-grained mathematical ideas. In short, our goal is to better understand the kinds of thinking provoked through the dynamic VRs and the ways in which working with the representations provokes rich discussion about the mathematics these teachers teach.
Examples Of Visual Representations
4. Do you have any emerging findings to share?
Not yet! We will be collecting data in the summer and fall.
Project Resources & Products:
Visual Representation Meaning
- Proportion Playground toys and dynamic representations are available at http://jamespburke.website/pplay_webfiles/
